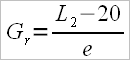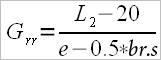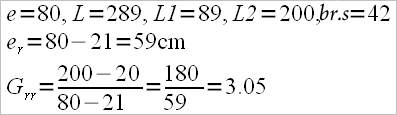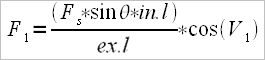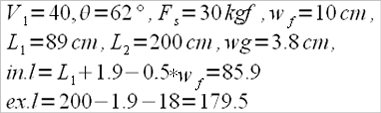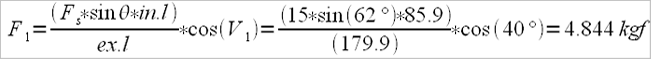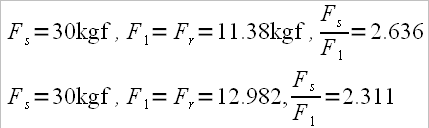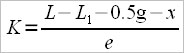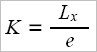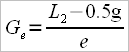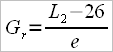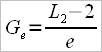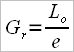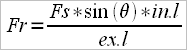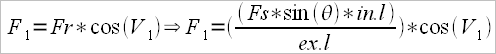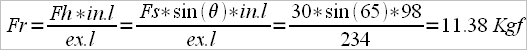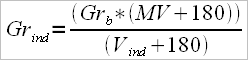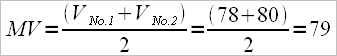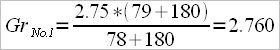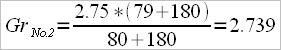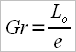Clarifying the notion of burden factor (drag factor) – Part three
Final Comments
After the previous conclusions we can say that the drag factor, at any moment while passing through the water, is actually the ratio of the pushing force against the stretcher (Fs) and the boat propulsion force (F1). We will note the drag factor with Dr.f, thus obtaining the formula:
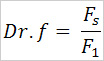
The burden factor will be different at catch compared to the perpendicular on the boat or compared to finish.
The lowest value of the drag factor will be in the oar’s perpendicular position onto the boat’s longitudinal axis, where we have maximum efficiency.
Dr. Valery Kleshnev, PhD in biomechanics, says: “The span/spread doesn’t affect the gearing. Decreasing the span/spread with 2cm (in a sculling boat, decreasing on one side is actually 1cm) will increase the catch angle by 0.5 degrees.”
The same increase of catch angle can be achieved through other methods: moving the stretcher or shortening the internal lever.
Now we are able to increase or decrease the total length of the oar by 10 -12 cm (not possible 20 years ago), this means that we can simplify how we find the drag factor (Dr.f), using fewer variables without the need to change at the same time the span/spread and the internal lever (ie total length of the oar).
The sequence of operation is:
1. Determination of the drag factor depending on the result on the ergometer – 2000 m
For example: for a result of 6 minutes – 2000 m, Dr.f will be 2.74 for “M2-” and 2.26 for “M1x” (calculated after the Australian model) and for a result of 7 min – 2000 m the Dr.f is 2.70 for “W2-” and 2.25 for “W1x”.
2. Measurement of the specific amplitude (leg length plus mobility) and taking into account the rower’s individual parameters: trunk height, shoulder breadth, fist width and the angle of the blade in finish position we will determine:
– rowing sector (total angle “V” from the catch to the end of the stroke) after the formula:A max : v max
– projection of the internal lever (R),
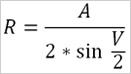
– span/spread (e)
Since the calculation of the drag factor proposed by me has the formula:
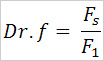
it involves the measuring device for the stretcher force, and a special measuring angle device used to measure the angle between the oar’s handle and the rower’s arm, which is possible only in national teams, we can either relate to the Australian method of calculation where we already have available the tables (rigging manual), especially since us, Romanians, use Crocker type oars. According to the formula:
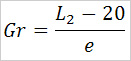
either to the calculation model of “gearing” proposed by mr. V. Kleshnev, namely the external lever (ex.l) divided by the effective internal lever (in.l)
ex.l =L2 – 2 – 18 and in.l = L1 + 2 – 0,5 f (scull oars)
ex.l = L2 – 2 – 24 and in.l = L1 + 2 – 2f (sweep oars where “0.5f” means half of the fist’s width and “2f” means twice the fist’s width)
In the first case, even if the Australian method is valid only for the orthogonal position of the oar, let’s remember that individualization has been already achieved by establishing the total angle (V), the projection of the internal lever (R) and the span/spread (e) depending by the specific amplitude (A) of each rower.
Should be noted that the real boat specific amplitude (length of stroke) is 6% lower than the measured specific amplitude (Lp + mobility) for sculling boats.
I chose to measure these two parameters (leg length and mobility) because one cannot cheat any more like in the case of directly measuring in the boat, where because of the desire to have a bigger amplitude, rower stretch excessively at attack or lean too much at finish.
In the second case, I would like to make a note of a similar model that I’ve encountered in “Topoergonomia in canotaj” (C. Radut, J. Billard) called the apparent lever ratio, but in that case the author only talked about the handle’s length (L1) and the external length of the oar, from the collar to the external end of the blade (L2).
The equivalent for 6 min. – 2000 m ergometer is “M2-” = 2.350 and “M1x” = 2.100, for 7 min. – 2000 m ergometer “W2-” = 2.300 and “W1x” 2.090.
For other boats there are also calculated tables.
When calculating the drag factor according to either the Carl Adam model, the English or the Australian model they do not include in the calculation the internal lever, but only the external lever, complete or incomplete, divided by the span / spread.
When calculating the drag factor according to Kleshnev’s formula he does not enter the calculation span / spread, but only the effective external lever (ext.l) divided by the effective internal lever (int. l).
Is to decide which one to choose, which one is better.