Continuation the notion of drag factor (burden factor) – Part Two

The propulsion force of the boat was already explained in the previous article but there I was referring only to sweep boats.

For scull boats the situation is somewhat different. If in the case of the sweep boats, the vector of the force applied at the handle overlapped the longitudinal axis of the boat, respectively half of the distance between the rower’s two shoulders, in the case of the scull boats this vector is placed on a line parallel to the longitudinal axis of the boat at a distance equal to half of the distance between the two shoulders.

The questions is: Why isn’t it confused with the longitudinal axis of the boat since the stretcher pushing force is exercised along to it?

The answer: Applied force is transmitted through the legs, trunk and arms. It is known that the leg’s strength is higher than the strength of the arms. The stroke’s charge will be felt in the shoulder joint, which means that we can push with the feet as much as the shoulder’s joint will allow us to (muscles, tendons, ligaments, joint capsule). As a reference we’ll take this line, parallel to the longitudinal axis, but because the action takes place symmetrically on both sides, the two vectors parallels to the shoulders lines can be considered componenets of the vector which pushes into the palonier along the longitudinal axis. This means that the span (spread) is actually smaller with half the width of the shoulders (shoulders breadth – Br.s).

Real spread (er) = Normal spread (e)- 0.5 * shoulders breadth (Br.s)
er = e – 0.5*Br.s

If we want to calculate after the Autralian model where

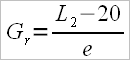
the formula becomes

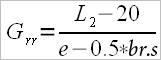
Example:

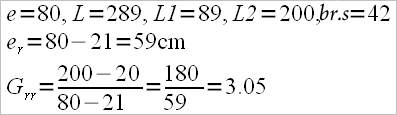
If we want to calculate the drag factor (burden factor) in it’s different momments, we’ll use the same formula as in the previous article:

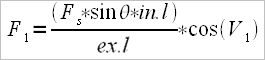
where now

(handle minus half the fist’s width, and theta is the angle between the handle and the longitudnial axis of the arm)

Note: in the formula there s “cos(V1)”, which means that the momment of the stroke for which we calculate it’s before the orthogonal pozition of the oar (toward the attack). If the momment for which we calculate is beyond the orthogonal position, meaning more towards the end of the stroke, then we’ll take into account cos(V2). For the orthogonal position, either of the two “cos(V1)” or “cos(V2)” aren’t necessary, because F1=Fr.

Regarding the stretcher pushing force, because the calculation is made for only a single oar, we’ll take into consideration 0.5Fs.

Example:

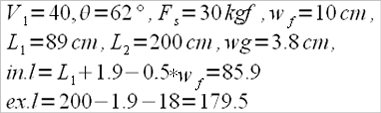
According to the formula:

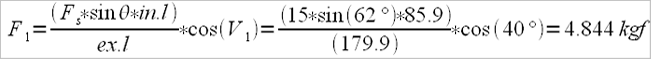
But, because we have calculated the draging (burdening) factor only to one oar (on one side), we’ll duble the result and get F1(total)=9.688Kgf

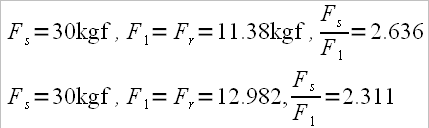
If we do a comparison to the calculation of a sweep boat as we did in the previous article we will notice that the ration between the stretcher pushing force (Fs)(Fs=30Kgf) and the orthogonal position propelling force (F1=Fr) will return some results that can be considered as “burdening coefficient” (drag factor)